reading-notes

Class-10: Stacks & Queues

What is a Stack

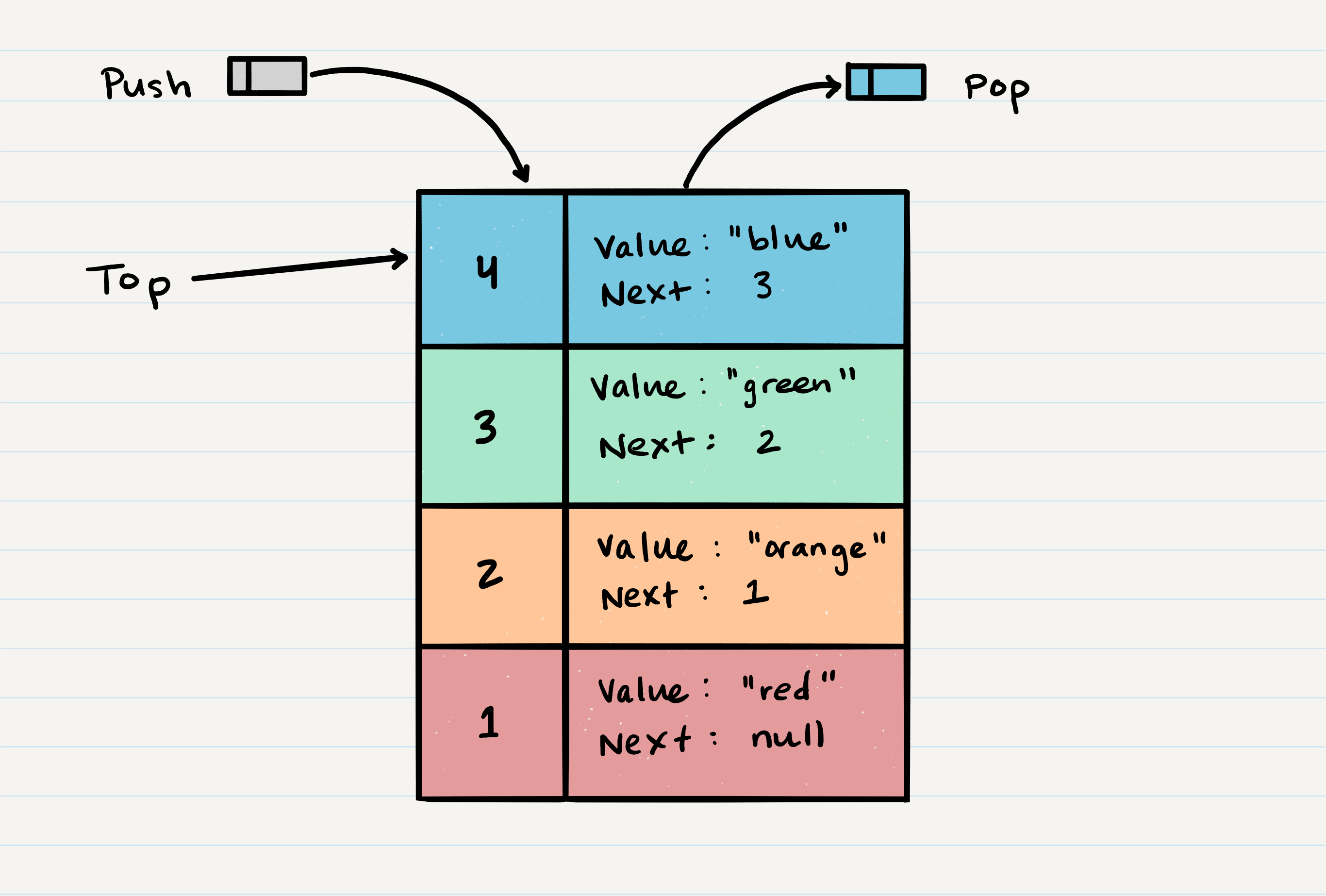
A stack is a data structure that consists of Nodes. Each Node references the next Node in the stack, but does not reference its previous.

Common terminology for a stack is

Push - Nodes or items that are put into the stack are pushed
Pop - Nodes or items that are removed from the stack are popped. When you attempt to pop an empty stack an exception will be raised.
Top - This is the top of the stack.
Peek - When you peek you will view the value of the top Node in the stack. When you attempt to peek an empty stack an exception will be raised.
IsEmpty - returns true when stack is empty otherwise returns false.

Stacks follow these concepts:

FILO - First In Last Out

This means that the first item added in the stack will be the last item popped out of the stack.

LIFO - Last In First Out

This means that the last item added to the stack will be the first item popped out of the stack.

Stack Visualization

the top most item is denoted as the top. When you push something to the stack, it becomes the new top. When you pop something from the stack, you pop the current top and set the next top as top.next.

Stack Example

Push O(1)

When adding a Node, you push it into the stack by assigning it as the new top, with its next property equal to the original top.

Pseudo Code For Push

ALOGORITHM push(value)
// INPUT <-- value to add, wrapped in Node internally
// OUTPUT <-- none
   node = new Node(value)
   node.next <-- Top
   top <-- Node

Pop O(1)

Popping a Node off a stack is the action of removing a Node from the top. When conducting a pop, the top Node will be re-assigned to the Node that lives below and the top Node is returned to the user.

Typically, you would check isEmpty before conducting a pop. This will ensure that an exception is not raised. Alternately, you can wrap the call in a try/catch block.

Pseudo Code For Pop

ALGORITHM pop()
// INPUT <-- No input
// OUTPUT <-- value of top Node in stack
// EXCEPTION if stack is empty

   Node temp <-- top
   top <-- top.next
   temp.next <-- null
   return temp.value

Peek O(1)

When conducting a peek, you will only be inspecting the top Node of the stack.

Pseudo code for a peek

ALGORITHM peek()
// INPUT <-- none
// OUTPUT <-- value of top Node in stack
// EXCEPTION if stack is empty

   return top.value

We do not re-assign the next property when we peek because we want to keep the reference to the next Node in the stack. This will allow the top to stay the top until we decide to pop.

IsEmpty O(1)

Pseudo code for isEmpty

ALGORITHM isEmpty()
// INPUT <-- none
// OUTPUT <-- boolean

return top = NULL

What is a Queue

Common terminology for a queue is

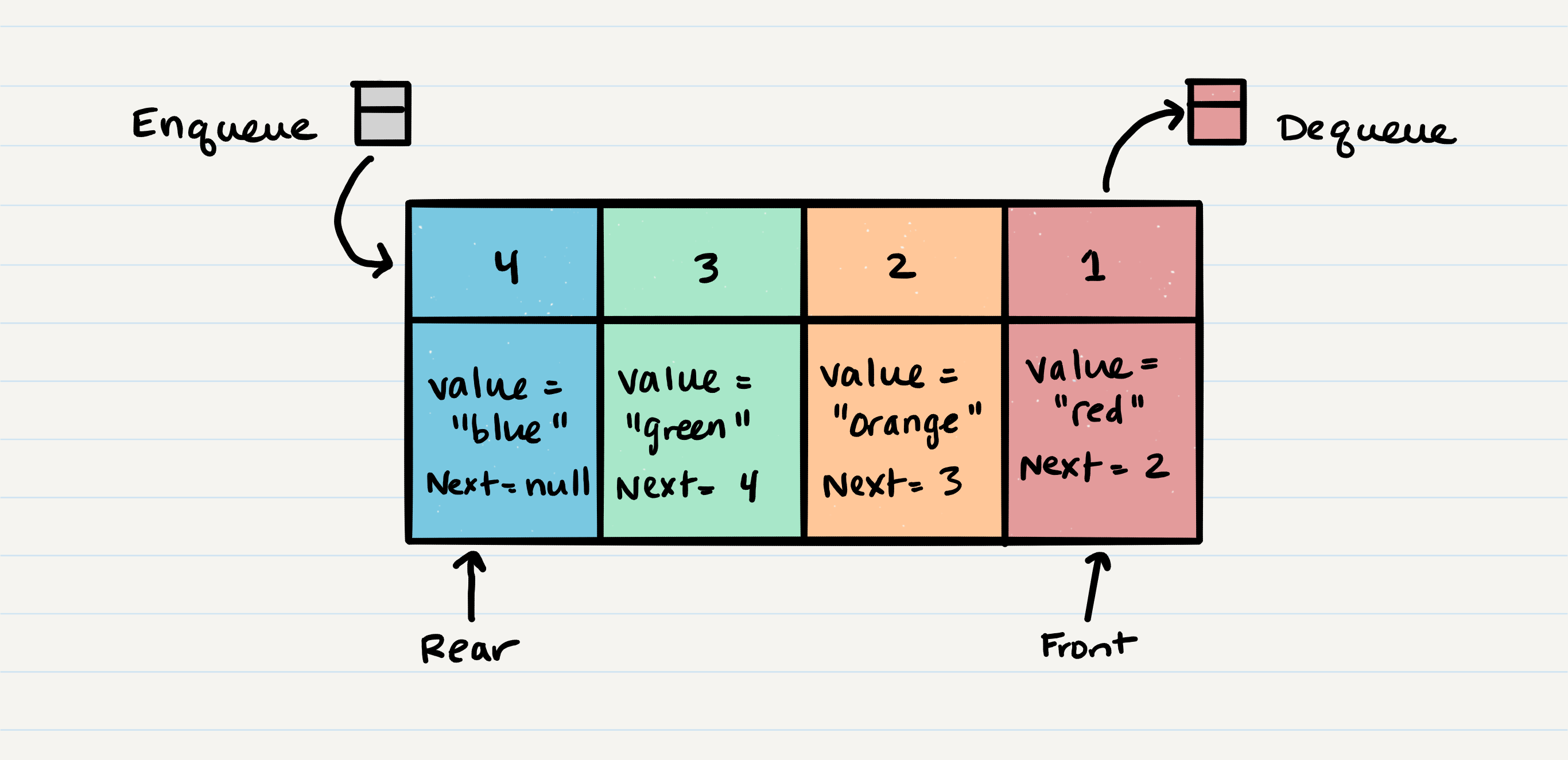
Enqueue - Nodes or items that are added to the queue.
Dequeue - Nodes or items that are removed from the queue. If called when the queue is empty an exception will be raised.
Front - This is the front/first Node of the queue.
Rear - This is the rear/last Node of the queue.
Peek - When you peek you will view the value of the front Node in the queue. If called when the queue is empty an exception will be raised.
IsEmpty - returns true when queue is empty otherwise returns false.

Queue Visualization

Queue Visualization

Enqueue O(1)

When you add an item to a queue, you use the enqueue action. This is done with an O(1) operation in time because it does not matter how many other items live in the queue (n); it takes the same amount of time to perform the operation.

Pseudo code for the enqueue

ALGORITHM enqueue(value)
// INPUT <-- value to add to queue (will be wrapped in Node internally)
// OUTPUT <-- none
   node = new Node(value)
   rear.next <-- node
   rear <-- node

Dequeue O(1)

When you remove an item from a queue, you use the dequeue action. This is done with an O(1) operation in time because it doesn’t matter how many other items are in the queue, you are always just removing the front Node of the queue.

Pseudo code for the dequeue

ALGORITHM dequeue()
// INPUT <-- none
// OUTPUT <-- value of the removed Node
// EXCEPTION if queue is empty

   Node temp <-- front
   front <-- front.next
   temp.next <-- null

   return temp.value

Peek O(1)

When conducting a peek, you will only be inspecting the front Node of the queue.

Pseudo code for a peek

ALGORITHM peek()
// INPUT <-- none
// OUTPUT <-- value of the front Node in Queue
// EXCEPTION if Queue is empty

   return front.value

We do not re-assign the next property when we peek because we want to keep the reference to the next Node in the queue. This will allow the front to stay in the front until we decide to dequeue

IsEmpty O(1)

Pseudo code for isEmpty

ALGORITHM isEmpty()
// INPUT <-- none
// OUTPUT <-- boolean

return front = NULL