reading-notes

Class 15: Trees (Binary Trees & Binary Search Trees)

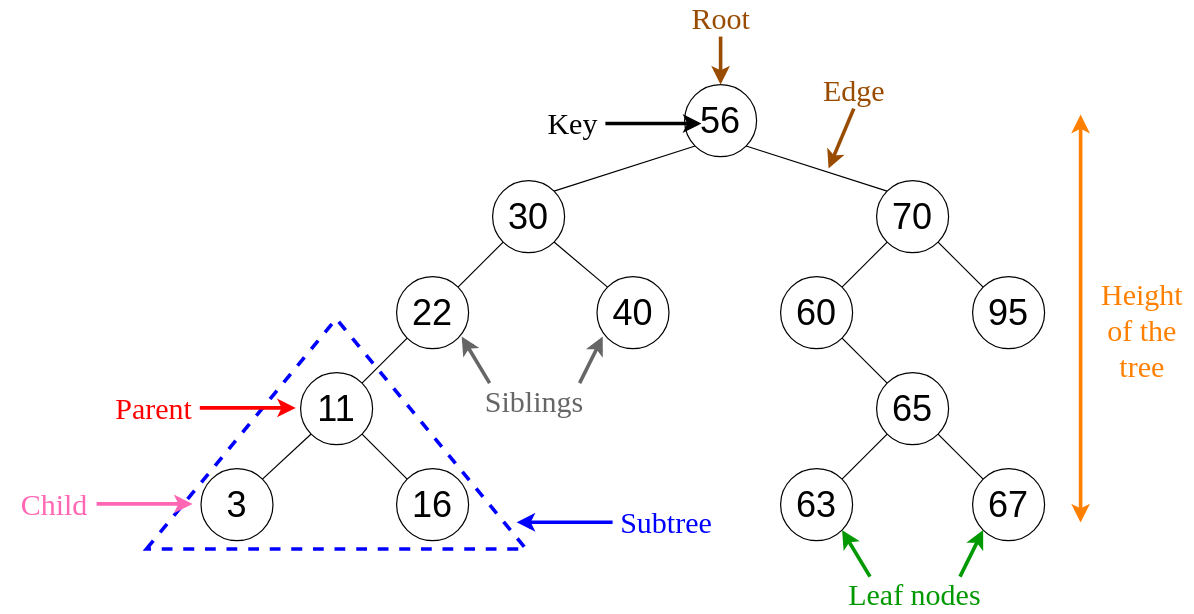
Trees

Common Terminology

• Node - A node is the individual item/data that makes up the data structure
• Root - The root is the first/top Node in the tree
• Left Child - The node that is positioned to the left of a root or node
• Right Child - The node that is positioned to the right of a root or node
• Edge - The edge in a tree is the link between a parent and child node
• Leaf - A leaf is a node that does not contain any children
• Height - The height of a tree is determined by the number of edges from the root to the bottommost node

Traversals

Depth First

Depth first traversal is where we prioritize going through the depth (height) of the tree first. There are multiple ways to carry out depth first traversal, and each method changes the order in which we search/print the root.

Ways that you can Traverse a tree

• Pre-order: root >> left >> right
• In-order: left >> root >> right
• Post-order: left >> right >> root

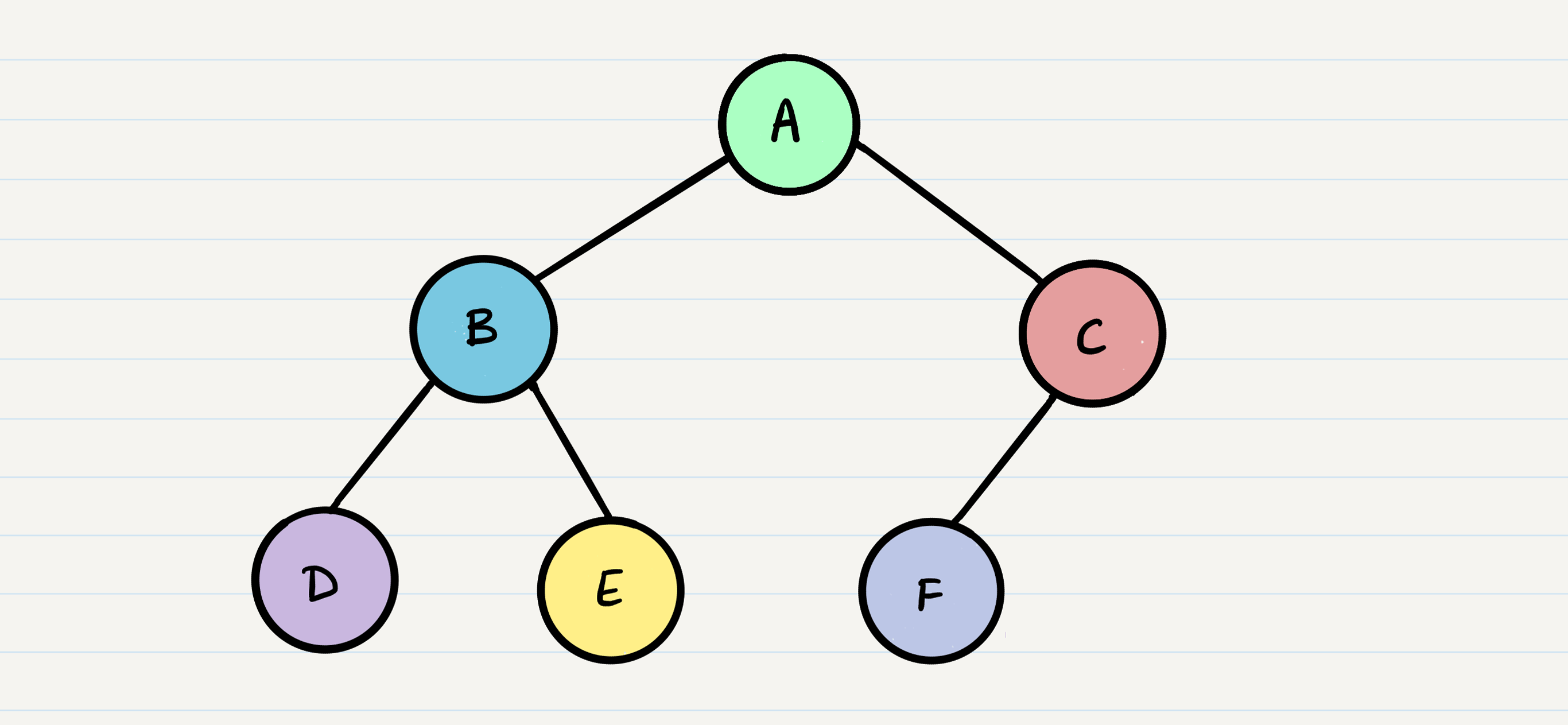
The various outputs for traversing this tree would look like these examples below:

• Pre-order: A, B, D, E, C, F
• In-order: D, B, E, A, F, C
• Post-order: D, E, B, F, C, A

Recursion is the best way to traverse through a tree. With these traversals, we rely on the call stack to navigate back up the tree when we have reached the end of a sub-path.

Pre-order pseudocode

ALGORITHM preOrder(root)

  OUTPUT <-- root.value

  if root.left is not NULL
      preOrder(root.left)

  if root.right is not NULL
      preOrder(root.right)

Pre-order means that the code should assgin the top value of the tree to the root value of the tree first and send that node through the function. Next, the code should look at the root.left and root.right values, if there is a values at root.leftthen it should send that node through the function, if not then it should send root.right through the function. As the function traverses the tree each value is added to a stack.

Your code should continue to do this until it reaches a leaf node (A leaf is a node that does not contain any children, or simply no left or right values).

The most recent value will pop off of the call stack and the root will be reassigned back to the previous root.

This is the heart of recursion: when we complete a function call, we pop it off the stack and are able to continue execution through the previous function call.

The code block will now pick up where it left off when the previous root was the current root. Since it already looked for root.left, it will now look for root.right.

Now that the root is checking the root.right value, if a value exists, that value will be added to the stack, and the node will be checked for both a root.left and a root.right.

This process will continue until it hits another leaf value, then it will pop values off the stack until it finds another root.right value that has not been checked.

This process will continue, of adding and popping values from the stack, until the entire Tree’s values have been checked.

Remember: You should always be checking both left and right but working with the left values until it hits a leaf and then be moving on to working with the right values!!!!

Pre-order

ALGORITHM preOrder(root)
// INPUT <-- root node
// OUTPUT <-- pre-order output of tree node's values

    OUTPUT <-- root.value

    if root.left is not Null
        preOrder(root.left)

    if root.right is not NULL
        preOrder(root.right)

In-order

ALGORITHM inOrder(root)
// INPUT <-- root node
// OUTPUT <-- in-order output of tree node's values

    if root.left is not NULL
        inOrder(root.left)

    OUTPUT <-- root.value

    if root.right is not NULL
        inOrder(root.right)

Post-order

ALGORITHM postOrder(root)
// INPUT <-- root node
// OUTPUT <-- post-order output of tree node's values

    if root.left is not NULL
        postOrder(root.left)

    if root.right is not NULL
        postOrder(root.right)

    OUTPUT <-- root.value

Notice the similarities between the three different traversals above. The biggest difference between each of the traversals is when you are looking at the root node.

Breadth First

Breadth first traversal iterates through the tree by going through each level of the tree node-by-node.

You’re going broad rather than deep.

You can possibly use a list and pop the values off as you go through, rather than using a queue.

Binary Search Trees

Everything on the left HAS to be amaller than the root node, and everything on the right HAS to be larger than the root node.

Good question for possible interview:

Is this tree balanced?